Latent Dirichlet allocation¶
Latent Dirichlet allocation (LDA, commonly known as a topic model) is a generative model for bags of words.
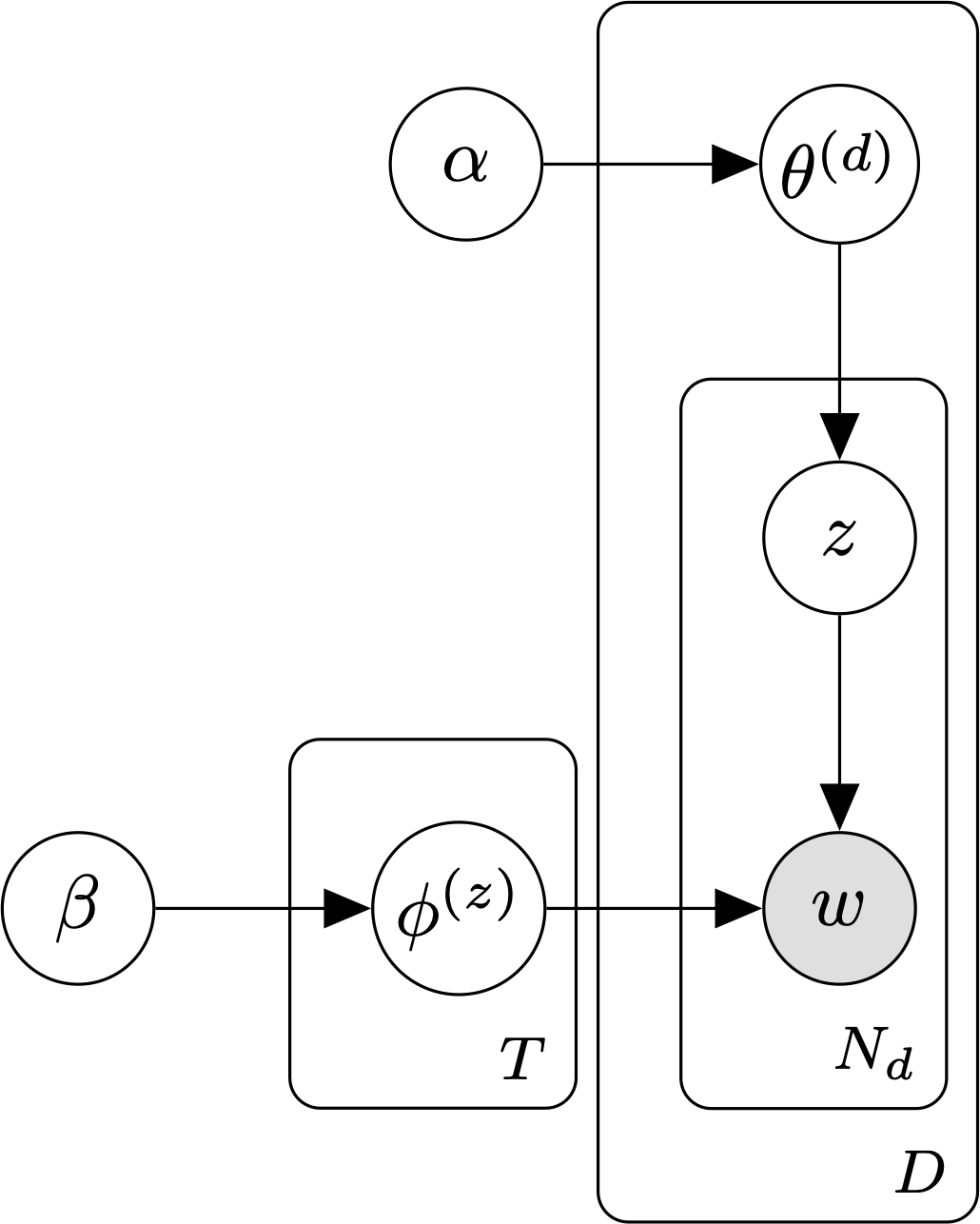
In LDA, each word in a piece of text is associated with one of T latent topics. A document is an unordered collection (bag) of words. During inference, the goal is to estimate probability of each word token under each topic, along with the per-document topic mixture weights, using only the observed text.
The parameters of the LDA model are:
- \(\theta\), the document-topic distribution. We use \(\theta^{(i)}\) to denote the parameters of the categorical distribution over topics associated with document \(i\).
- \(\phi\), the topic-word distribution. We use \(\phi^{(j)}\) to denote the parameters of the categorical distribution over words associated with topic \(j\).
The standard LDA model [1] places a Dirichlet prior on \(\theta\):
The smoothed/fully-Bayesian LDA model [2] adds an additional Dirichlet prior on \(\phi\):
To generate a document with the smoothed LDA model, we:
- Sample the parameters for the distribution over topics, \(\theta \sim \text{Dir}(\alpha)\).
- Sample a topic, \(z \sim \text{Cat}(\theta)\).
- If we haven’t already, sample the parameters for topic z’s categorical distribution over words, \(\phi^{(z)} \sim \text{Dir}(\beta)\).
- Sample a word, \(w \sim \text{Cat}(\phi^{(z)})\).
- Repeat steps 2 through 4 until we have a bag of N words.
The joint distribution over words, topics, \(\theta\), and \(\phi\) under the smoothed LDA model is:
The parameters of the LDA model can be learned using variational expectation maximization or Markov chain Monte Carlo (e.g., collapsed Gibbs sampling).
Models
References
| [1] | Blei, D., Ng, A., & Jordan, M. (2003). “Latent Dirichlet allocation”. Journal of Machine Learning Research, 3, 993–1022. |
| [2] | Griffiths, T. & Steyvers, M. (2004). “Finding scientific topics”. PNAS, 101(1), 5228-5235. |