Neural networks¶
The neural network module includes common building blocks for implementing modern deep learning models.
Layers
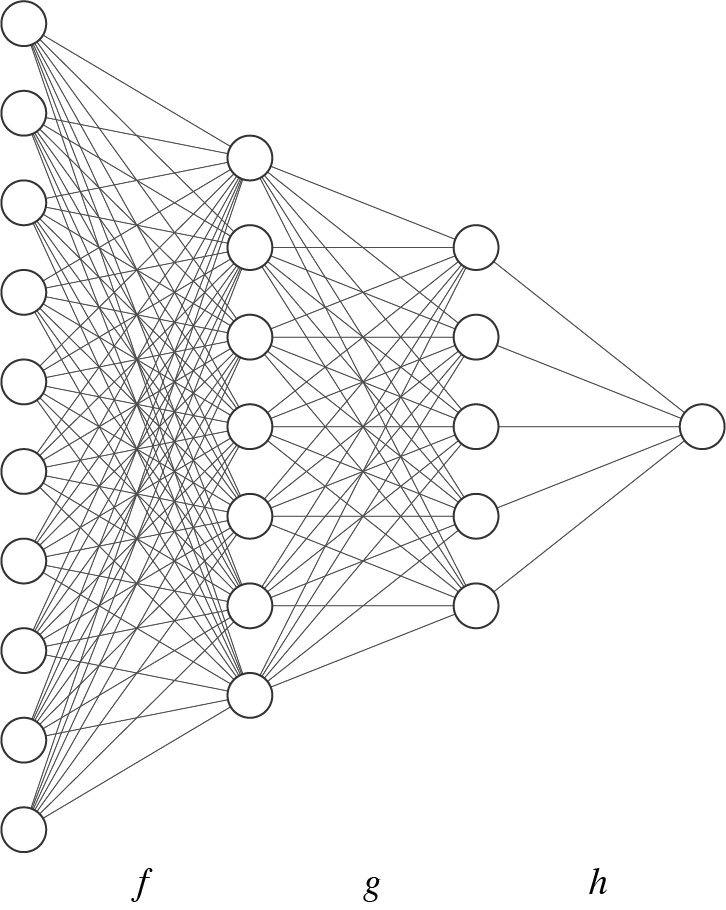
Most modern neural networks can be represented as a composition of many small, parametric functions. The functions in this composition are commonly referred to as the “layers” of the network. As an example, the multilayer perceptron (MLP) below computes the function \((f \circ g \circ h)\) where, f, g, and h are the individual network layers.
Many neural network layers are parametric: they express different transformations depending on the setting of their weights (coefficients), biases (intercepts), and/or other tunable values. These parameters are adjusted during training to improve the performance of the network on a particular metric.
The Layers module contains a number of common transformations that can be composed to create larger networks.
Layers
Activations
Each unit in a neural network sums its input and passes it through an activation function before sending it on to its outgoing weights. Activation functions in most modern networks are real-valued, non-linear functions that are computationally inexpensive to compute and easily differentiable.
The Activations module contains a number of common activation functions.
Activations
Losses
Training a neural network involves searching for layer parameters that optimize the network’s performance on a given task. Loss functions are the quantitative metric we use to measure how well the network is performing. Loss functions are typically scalar-valued functions of a network’s output on some training data.
The Losses module contains loss functions for a number of common tasks.
Losses
Optimizers
The Optimizers module contains several popular gradient-based strategies for adjusting the parameters of a neural network to optimize a loss function. The proper choice of optimization strategy can help reduce training time / speed up convergence, though see [1] for a discussion on the generalization performance of the solutions identified via different strategies.
| [1] | Wilson, A. C., Roelofs, R., Stern, M., Srebro, M., & Recht, B. (2017) “The marginal value of adaptive gradient methods in machine learning”, Proceedings of the 31st Conference on Neural Information Processing Systems. https://arxiv.org/pdf/1705.08292.pdf |
Optimizers
Learning Rate Schedulers
It is common to reduce an optimizer’s learning rate(s) over the course of training in order to eke out additional performance improvements. The Schedulers module contains several strategies for automatically adjusting the learning rate as a function of the number of elapsed training steps.
Schedulers
Wrappers
The Wrappers module contains classes that wrap or otherwise modify the behavior of a network layer.
Wrappers
Modules
Many deep networks consist of stacks of repeated modules. These modules, often consisting of several layers / layer operations, can themselves be abstracted in order to simplify the building of more complex networks. The Modules module contains a few common architectural patterns that appear across a number of popular deep learning approaches.
Modules
Full Networks
The Models module contains implementations of several well-known neural networks from recent papers.
Full Networks
Utilities
The Utilities module contains a number of helper functions for dealing with weight initialization, convolution arithmetic, padding, and minibatching.
Utilities